数组排序

发表于 分类于 阅读次数： 本文字数： 2.4k 阅读时长 ≈ 4 分钟

LeetCode原题
难度 中等

给你一个整数数组 nums，将该数组升序排列。

示例 1：

输入：nums = [5,2,3,1]
输出：[1,2,3,5]

示例 2：

输入：nums = [5,1,1,2,0,0]
输出：[0,0,1,1,2,5]

提示：

1 <= nums.length <= 50000
-50000 <= nums[i] <= 50000

这道题在LeetCode中难度是中等，可能看上去很简单，因为我们随手可以写出的排序算法就有很多种，但是如果想要牢靠掌握所有的排序算法还是够得上中等难度的。

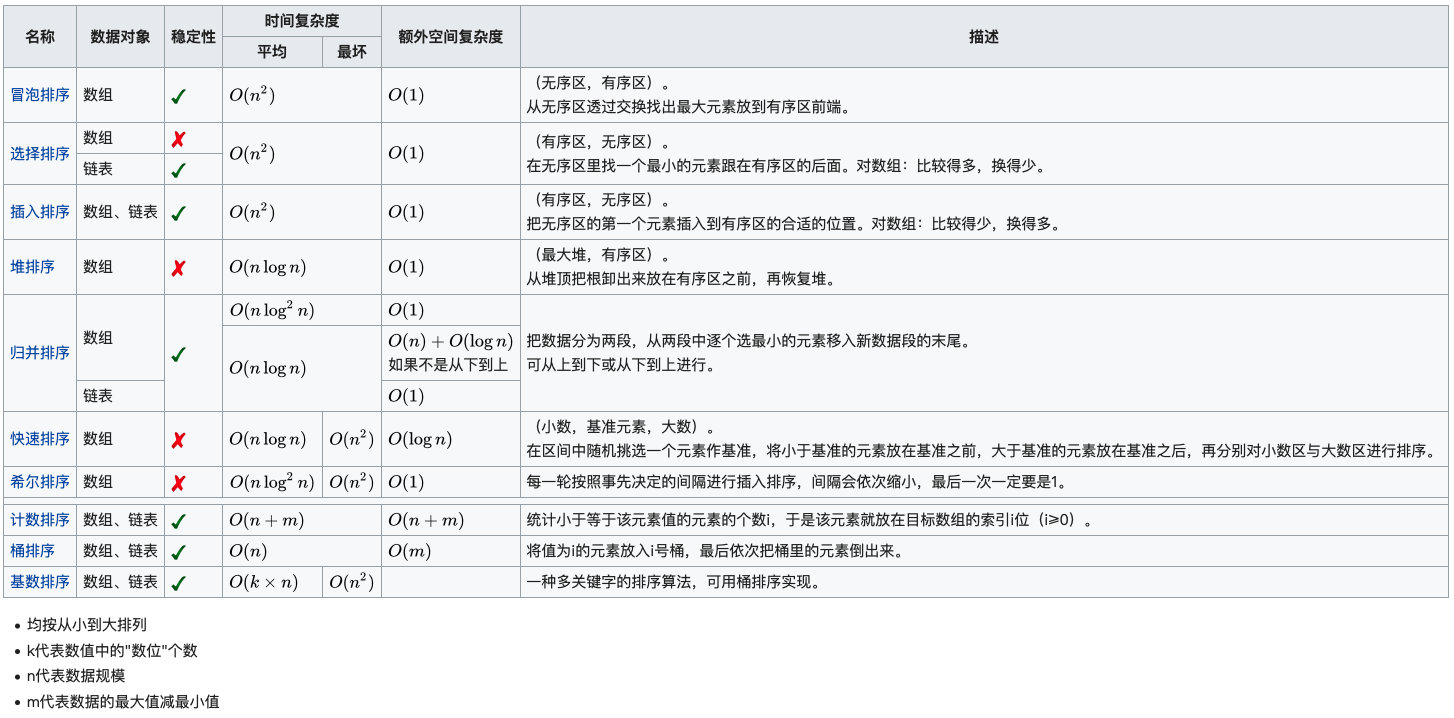
下面是几种常用算法的整理：

快速排序

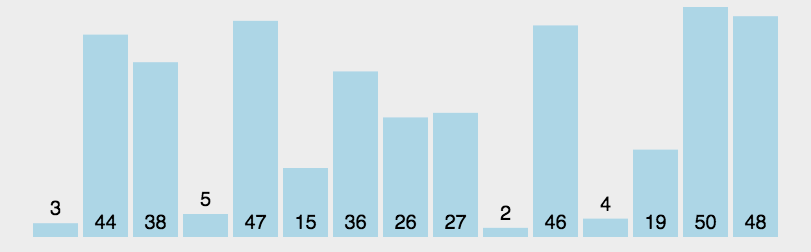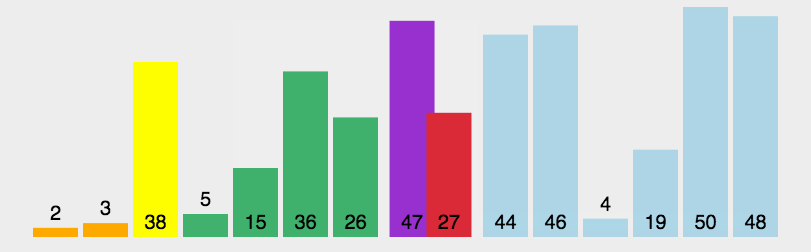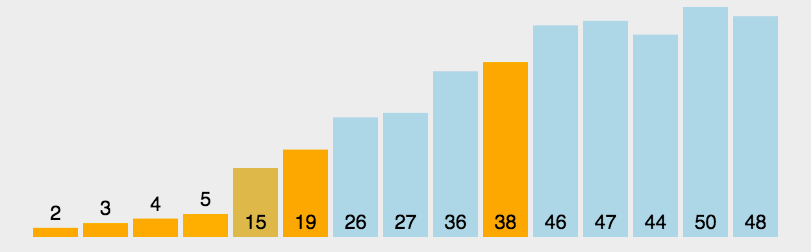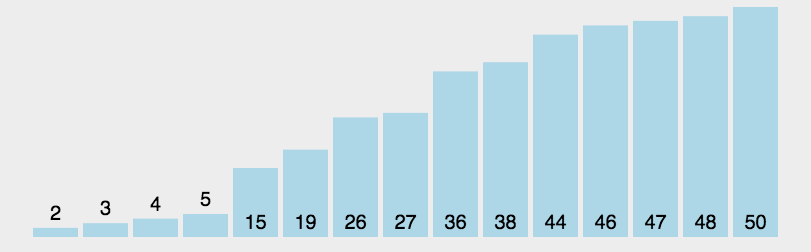
快排是最常用的几种排序方法之一，其主要方法是

  1. 在数组中随机选择一个数作为基准，将该基准放到数组的末端。

  2. 将数组中所有数与基准进行对比，将大于基准的数移动至基准的右侧。

  3. 将数组左侧和右侧分别试做两个新数组重复步骤1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
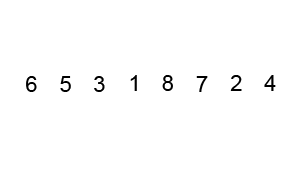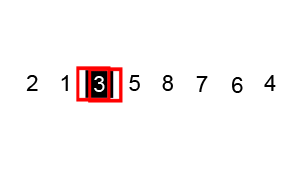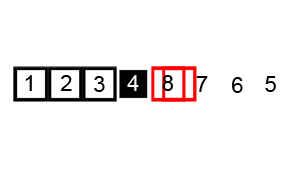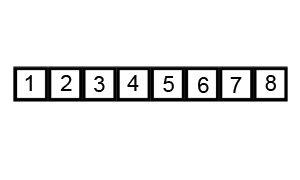
24
class Solution:
    def partition(self, nums, l, r):
        pivot = nums[l]
        while l < r:
            while l < r and pivot <= nums[r]:
                r -= 1
            nums[l] = nums[r] 
            while l < r and nums[l] <= pivot:
                l += 1 
            nums[r] = nums[l]
        nums[l] = pivot
        return l
    def random_partition(self, nums, l, r):
        i = random.randint(l, r)
        nums[i], nums[r] = nums[r], nums[i]  
        return self.partition(nums, l, r)
    def quickSort(self, nums, l, r):
        if l < r:
            k = self.random_partition(nums, l, r)
            self.quickSort(nums, l, k-1)
            self.quickSort(nums, k+1, r)
    def sortArray(self, nums: List[int]) -> List[int]:
        self.quickSort(nums, 0, len(nums)-1 )
        return nums

归并排序

归并排序的主要思想是递归+重排两个有序数组

  1. 将数组分成两个部分数组，对返回的两个有序数组进行排序

  2. 如果部分数组中只有一个元素，直接返回，否则进行步骤1

  3. 对两部分分别进行merge，返回排序后的数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
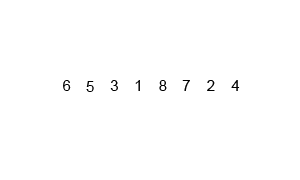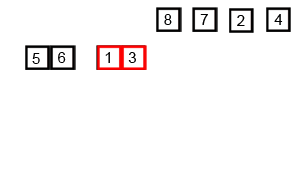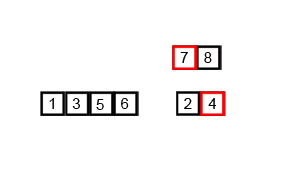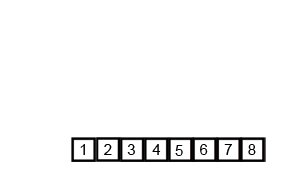
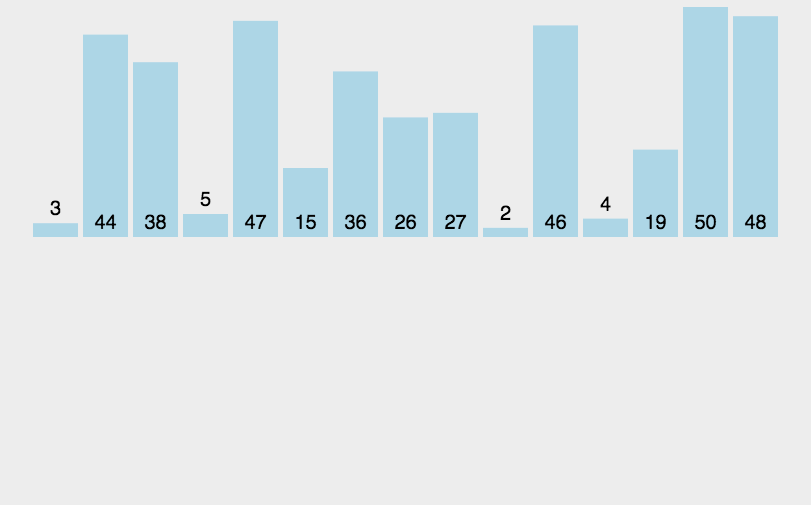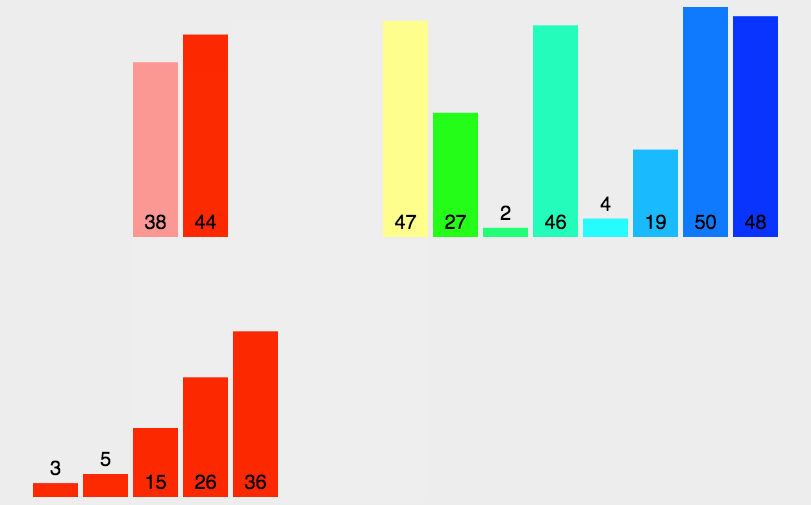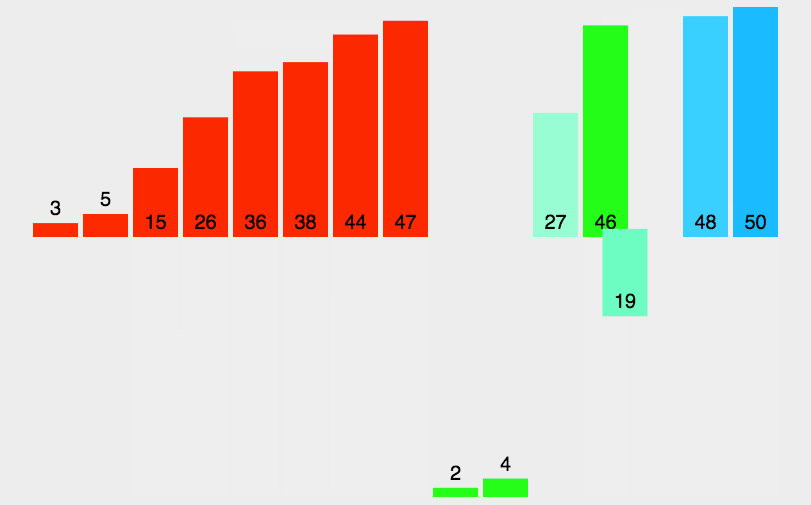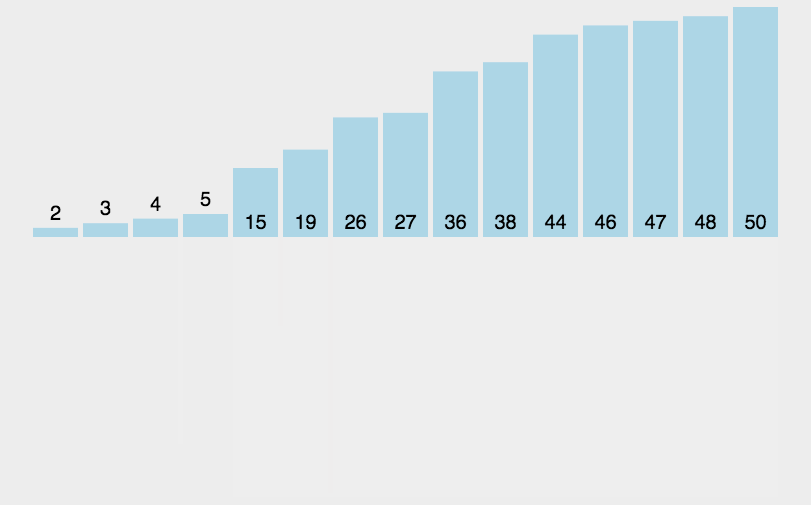
18
class Solution:

    def sortArray(self, nums: List[int]) -> List[int]:
        if len(nums) == 1: 
            return nums
        mid = len(nums) // 2
        return merge(self.sortArray(nums[:mid]), self.sortArray(nums[mid:]))

    def merge(self, left, right):
        res = []
        while len(left) > 0 and len(right) > 0:
            if left[0] < right[0]:
                res.append(left.pop(0))
            else:
                res.append(right.pop(0))
        res += left
        res += right
        return res

堆排序

堆排序是基于堆这种数据结构所设计的排序算法

  1. 建堆，从底向上调整堆，使得父亲节点比孩子节点值大，构成大顶堆

  2. 交换堆顶和最后一个元素，重新调整堆。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
def heap_sort(nums):
    # 调整堆
    # 迭代写法
    def adjust_heap(nums, startpos, endpos):
        newitem = nums[startpos]
        pos = startpos
        childpos = pos * 2 + 1
        while childpos < endpos:
            rightpos = childpos + 1
            if rightpos < endpos and nums[rightpos] >= nums[childpos]:
                childpos = rightpos
            if newitem < nums[childpos]:
                nums[pos] = nums[childpos]
                pos = childpos
                childpos = pos * 2 + 1
            else:
                break
        nums[pos] = newitem
    
    # 递归写法
    def adjust_heap(nums, startpos, endpos):
        pos = startpos
        chilidpos = pos * 2 + 1
        if chilidpos < endpos:
            rightpos = chilidpos + 1
            if rightpos < endpos and nums[rightpos] > nums[chilidpos]:
                chilidpos = rightpos
            if nums[chilidpos] > nums[pos]:
                nums[pos], nums[chilidpos] = nums[chilidpos], nums[pos]
                adjust_heap(nums, pos, endpos)

    n = len(nums)
    # 建堆
    for i in reversed(range(n // 2)):
        adjust_heap(nums, i, n)
    # 调整堆
    for i in range(n - 1, -1, -1):
        nums[0], nums[i] = nums[i], nums[0]
        adjust_heap(nums, 0, i)
    return nums